核物理入门

stardust

  最近有些忙，所以没发帖，现在有时间了，发一个新帖。


核的结构
  原子核由质子中子这些稳定粒子，和不稳定的介子等粒子组成。为了描述核的结构，提出了很多种模型，但是我们依然对核的结构知之甚少，不知道核的真实结构，核的狄拉克方程太难解，而且核的能级太高，薛定谔方程难以近似，而且多体薛定谔方程也只能近似，解不出来。最早的是液滴模型，就是认为核是一滴“核液体”，受到类似分子间力的力，也就是核的结合能是体积能减去表面能、库伦斥力、质子和中子间配对能（反对称能）最后加上质子、中子自身的配对能。体积能与体积成正比，也就是与重子数（质子和中子的总数）A成正比；表面能与表面积成正比，也就是与\(A^{\frac{2}{3}}\)成正比；库伦斥力也就是电势能，与电荷乘积成正比，与距离成反比，因为电荷正比于质子数Z，质子受到的排斥又是与其他质子的数量Z-1成正比所以正比于\(Z(Z-1)A^{-\frac{1}{3}}\)；而质子和中子间配对能项正比于两者的数量差的平方，同时与体积成反比，可以理解为是质子受中子作用同时中子也受质子作用，同时体积越大两者越分散，作用越小，也可以理解为是正比于方差，\((A-2Z)^2A^{-1}\)；还有一项质子-质子配对和中子-中子配对，一般选取能量原点两者都配对是正的，都不配对是负的，一个配对一个不配对是0，经验上正比于\(A^{-\frac{3}{4}}\)。最后得到的半经验公式是：$$E=a_VA-a_SA^{\frac{2}{3}}-a_cZ(Z-1)A^{-\frac{1}{3}}-a_A(A-2Z)^2A^{-1}+\left\{\begin{aligned}+a_PA^{-\frac{3}{4}}\\0\\-a_PA^{-\frac{3}{4}} \end{aligned}\right.$$
  比结合能是：$$B=a_V-a_SA^{-\frac{1}{3}}-a_cZ(Z-1)A^{-\frac{4}{3}}-a_A(A-2Z)^2A^{-2}+\left\{\begin{aligned}+a_PA^{-\frac{7}{4}}\\0\\-a_PA^{-\frac{7}{4}} \end{aligned}\right.
$$
  实验得到数值\(a_V\approx15.6{\rm MeV},a_S\approx16.8{\rm MeV},a_c\approx0.72{\rm MeV},a_A\approx23.3{\rm MeV},a_P\approx34{\rm MeV}\)，符合的比较好。

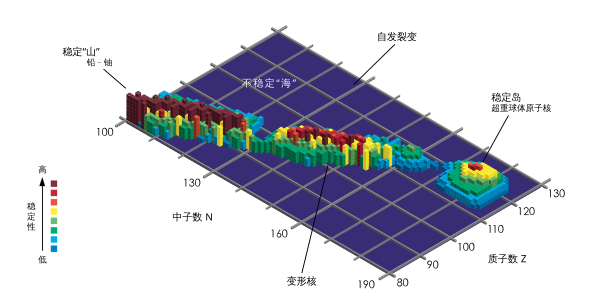
  核的稳定谷和可能的稳定岛

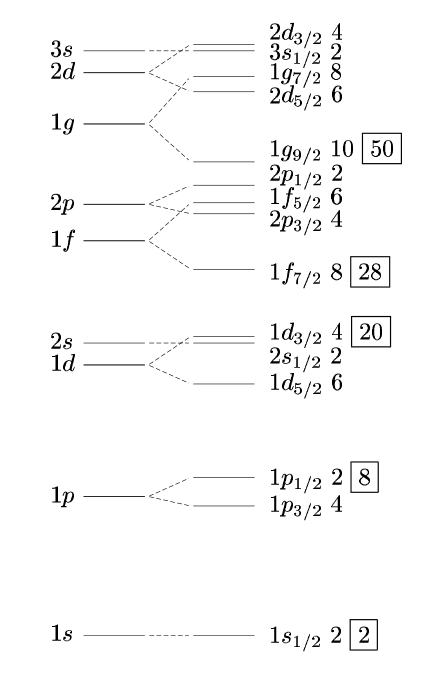
  但是液滴模型不符合量子力学，没有量子化，而核是量子化的，核反应放出的γ射线就是核的能级跃迁放出的，所以就有了类似于原子的外层电子的壳层模型。壳层模型也使用了一个近似，就是三维谐振子，谐振子的方程很简单，就是\(E\psi(r,\theta,\varphi)=\left(-\frac{\hbar^2}{2m}\nabla^2+\frac{1}{2}m\omega^2r^2\right)\psi(r,\theta,\varphi)\)，或者\(E\psi(x,y,z)=\left(-\frac{\hbar^2}{2m}\nabla^2+\frac{1}{2}m\omega^2(x^2+y^2+z^2)\right)\psi(x,y,z)\)。对于这个方程，解很复杂，但是可以认为三个方向的振动独立。能量\(E=[(N_x+\frac{1}{2})+(N_y+\frac{1}{2})+(N_z+\frac{1}{2})]\hbar\omega=(N+\frac{3}{2})\hbar\omega\)，其中\(N=N_x+N_y+N_z\)，同一能量有多种组合方式，能级的组合方式数也就是简并度为\(\frac{1}{2}(N+1)(N+2)\)，这是因为可以认为是分成三份，等效为插两块板子，或者说N+2中取出2。对于因为谐振子径向和角向运动独立，所以角量子数和径向量子数无关。为了达到这个简并度，可以认为N=2n+l+2，也就是角量子数增加2相当于径向量子数增加1，这种能级交错的方式符合规律。这就导致了幻数的出现，幻数核因为轨道满所以稳定，就像稀有气体稳定一样。但是因为有自旋，所以会出现自旋轨道耦合现象，自旋和公转同向的反向的能量不一致。同向低于反向，导致进一步能级交错，产生幻数变为2、8、20、28、50、82、126。

  后来还出现了更复杂的模型，尼尔逊模型就是，因为原子核可以不是正球体而是椭球体，这样可以进一步分裂轨道，改变能级排布降低能量，类似于化学上的姜-泰勒效应，分子发生形变降低总能量，有两级缩短赤道拉长的银离子，也有两级拉长赤道缩短的铜离子，所以银离子趋于二配位而铜离子趋于四配位，而且都不是标准的六配位。此外，整个核会有角动量，还会导致科里奥利力，能级进一步复杂化。

  而且有越来越多的证据表名原子核有类似分子的复杂结构，例如“晕核”，少数质子或中子容易被轰出去，所以结构近似为几个独立的质子或中子和核和主体构成，独立的重子围绕在核周围，有的核例如\(^9Be\)，容易轰成中子和三个氦核，所以认为是这三部分组成的，还有\(^12C\)主要由三个氦核的3α反应生成，可以认为是三个氦核构成的……核反应的产物比例，很大程度反应了核的结构。核的结构和化学一样复杂，但是我们却不知道。

核反应
  核反应有核衰变、核裂变和核聚变。核反应要克服巨大的势垒，核衰变中的一部分例如α衰变，可以认为是裂变的特殊形式。核裂变需要克服强力（核力），而核聚变需要克服库伦斥力。克服这些力很困难，所以核反应可以认为是通过隧穿完成的。薛定谔方程为\(\frac{\hbar^2}{2m}\frac{{\rm d}^2\psi}{{\rm d}x^2}=(V(r)-E)\psi\)，因为隧穿段很段，所以可以把势能近似为常数，这时可以认为解是指数函数，这种一边是简单导数一边是常数的都是指数，观查到解为\(\psi=\psi_0e^{-\sqrt{\frac{2m}{\hbar^2}}\int_R^b(V(r)-E)}\)，其中R为核的半径，b为势能等于系统能量的平衡点，也就是势垒的外边界。发生反应的概率为\(P=\psi^2=\psi_0^2e^{-2\sqrt{\frac{2m}{\hbar^2}}\int_R^b(V(r)-E)}=\psi_0^2e^{-2G}\)，G为核反应的伽莫夫因子。

  对于衰变或者裂变的近似，可以认为\(V(r)=E\frac{b}{r}\)，势能与距离成反比，而b处的势能就是系统能量。带根号积分一般要三角换元，换元\(r=b\sin^2\theta\)，得到积分\(\int^b_R\sqrt{\frac{b}{r}-1}{\rm d}r\approx \int^b_0\sqrt{\frac{b}{r}-1}{\rm d}r=\int^\frac{\pi}{2}_0\sqrt{\frac{b}{b\sin^2\theta}-1}{\rm d}(b\sin^2\theta)=\int^\frac{\pi}{2}_0\sqrt{\frac{1}{\sin^2\theta}-1}b\sin2\theta{\rm d}\theta=b\int^\frac{\pi}{2}_02\cos^2\theta{\rm d}\theta=\left.b(\frac{1}{2}\sin2\theta+\theta)\right|^\frac{\pi}{2}_0=\frac{b\pi}{2}\)，同时运用\(E=\frac{Z_1Z_2e^2}{4\pi\varepsilon_0b},b=\frac{Z_1Z_2e^2}{4\pi\varepsilon_0E}\)。也就得到了伽莫夫因子\(G=\sqrt{\frac{2mE}{\hbar^2}}\frac{b\pi}{2}=\sqrt{\frac{2mE}{\hbar^2}}\frac{\pi}{2}\frac{Z_1Z_2e^2}{4\pi\varepsilon_0E}=\sqrt{\frac{2m}{\hbar^2E}}\frac{Z_1Z_2e^2}{8\varepsilon_0}\)，这样就可以得到反应率。

核聚变
  核聚变远远比核裂变复杂，公式倒是不是太复杂，这过于简单了。首先是需要核聚变的碰撞截面，碰撞截面\(\sigma_f\approx\pi\lambda^2=\pi\frac{\hbar^2}{p^2}=\frac{\pi\hbar^2}{2mE}\propto \frac{1}{E}\)，碰撞截面决定了反应率，也就是正比于隧穿概率，所以\(\sigma_f=\frac{S(E)}{E}e^{-2G(E)}\)，其中S(E)就是碰撞截面关于核结构的修正项，实验获得，也有半经验公式。伽莫夫因子和裂变、衰变一样，整理一下：$$G=\sqrt{\frac{2\mu}{\hbar^2E}}\frac{Z_1Z_2e^2}{8\varepsilon_0}=\frac{1}{2}\sqrt{\frac{2\pi^2\mu}{E}}\frac{e^2}{4\pi\varepsilon_0\hbar}Z_1Z_2=\frac{1}{2}\sqrt{\frac{2\pi^2\mu}{E}}\alpha Z_1Z_2=\frac{1}{2}\sqrt{\frac{E_G}{E}}$$
  其中\(\alpha=\frac{e^2}{4\pi\varepsilon_0\hbar}\)被成为精细结构常数，近似为\(\frac{1}{137}\)，决定了电磁力的大小，最重要的常数之一，而\(E_G=2\pi^2\alpha^2\mu(Z_1Z_2)^2\)具有能量量纲，被称为伽莫夫能量，这个能量类似化学上的活化能。

  对于聚变率的计算，如果是两个粒子数对撞，很好计算，所有对面粒子的碰撞截面扫过的体积\(\sigma_f l\)在总体积中的占比就是单个粒子的聚变概率，因为碰撞截面不能重叠，所以碰撞截面乘上粒子数密度\(n_2\)再乘上经过距离\({\rm d}l=v{\rm d}t\)就是单个粒子的聚变概率，乘上本侧粒子的数量密度\(n_1\)，就是单位体积的聚变率就是\(R_f=n_1n_2\sigma_f(E)v\)，因为量子效应如果是同种粒子还要乘\(\frac{1}{2}\)，变成\(R_f=\frac{1}{2}n_1n_2\sigma_f(E)v\)。对于一定范围内气体，计算要复杂一些，以其中某个分子为坐标系，可以认为和静坐标系一样，分子遵从麦克斯韦速率分布,但是只有反向运动才能反应，所以要乘\(\frac{1}{2}\)。所以，体积项要放入麦克斯韦分布积分，或者说是点乘速率分布函数，也就是：$$R_f=n_1n_2\frac{1}{2}\int^{\infty}_0\sigma_f(E)v\left(\frac{\mu}{2\pi k_BT}\right)^{\frac{3}{2}}e^{-\frac{E}{k_{\scriptsize B}T}}4\pi v^2{\rm d}v=n_1n_2\sqrt{\frac{2}{\pi\mu k_B^3T^3}}\int^{\infty}_0\sigma_f(E)e^{-\frac{E}{k_{\scriptsize B}T}}E{\rm d}E$$
  代入碰撞截面表达式，得到：$$R_f=n_1n_2\sqrt{\frac{2}{\pi\mu k_B^3T^3}}\int^{\infty}_0\frac{S(E)}{E}e^{-\sqrt{\frac{E_{\scriptsize G}}{E}}}e^{-\frac{E}{k_{\scriptsize B}T}}E{\rm d}E=n_1n_2\sqrt{\frac{2}{\pi\mu k_B^3T^3}}\int^{\infty}_0S(E)e^{-\sqrt{\frac{E_{\scriptsize G}}{E}}-\frac{E}{k_{\scriptsize B}T}}{\rm d}E$$
  积分只能近似计算，运用最速下降法。近似S为常数，E值取最大值\(E_m\)，同时运用泰勒展开，得到：$$\int^{\infty}_0S(E_m)e^{f(E)}{\rm d}E\approx S(E_m)\int^{\infty}_0e^{f(E_m)-\frac{1}{2}|f''(E_m)|(E-E_m)^2}{\rm d}E\approx e^{f(E_m)}S(E_m)\int^{\infty}_{-\infty}e^{-\frac{1}{2}|f''(E_m)|E^2}=e^{f(E_m)}S(E_m)\sqrt{\frac{2\pi}{|f''(E_M)|}}$$
  不难计算\(E_m=\sqrt[{\LARGE 3}]{\frac{E_GT^2}{4}},f''(E_m)=-3\sqrt[{\LARGE 3}]{\frac{1}{2E_GT^5}}\)，伽莫夫峰的宽度为\(\frac{1}{\sqrt{|f''(E_m)|}}=\frac{1}{\sqrt{3}}\sqrt[{\Large 6}]{2E_GT^5}\)，最后得到聚变率：$$R_f=n_1n_2\sqrt{\frac{2}{\pi\mu k_B^3T^3}}e^{f(E_m)}S(E_m)\sqrt{\frac{2\pi}{|f''(E_M)|}}=n_1n_2\frac{2\sqrt[6]{2E_G}}{\sqrt{3\mu k_B^3}T^{\frac{2}{3}}}S(E_m)e^{-3\sqrt[3]{\frac{1}{2E_GT^5}}}$$
  天体物理有近似\(R_f\propto T^n\)，用幂函数近似。天体物理很多时候数量级对就行（真的，不是夸张）。计算可以得到不同核反应需要的温度，质子间的反应p-p链温度可以较低，所以太阳等小质量恒星以p-p链为主，而碳氮氧循环的温度需求高，同时碳氮氧循环活化熵低，所以大质量恒星以碳氮氧循环为主。

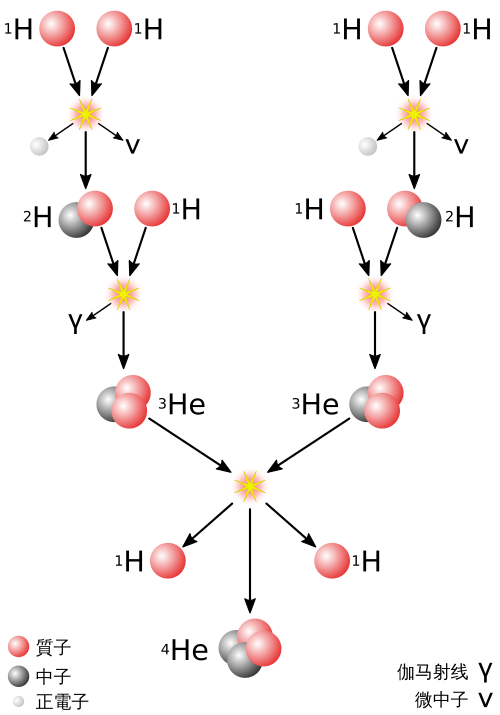
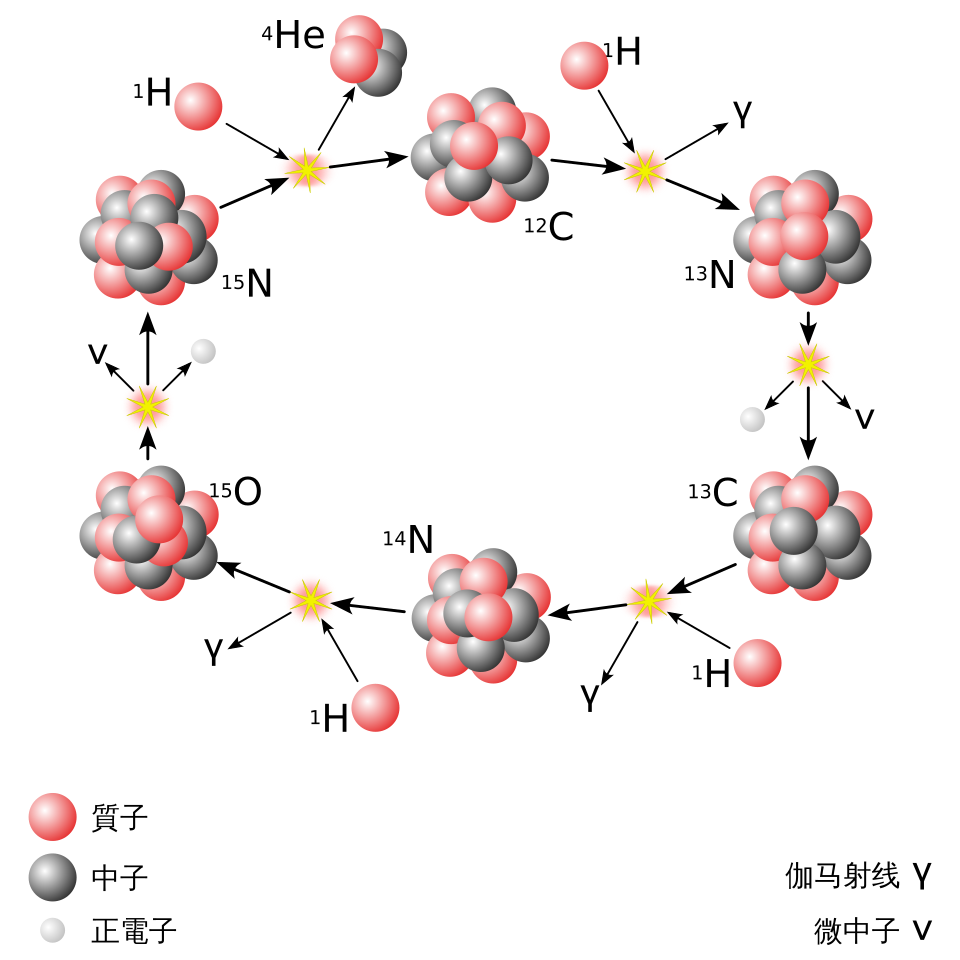
  p-p链和碳氮氧循环

  核聚变的活化熵目前知道的比较少，因为对核的结构了解太少。如果找到了活化熵极大的催化剂，冷核聚变不是梦，但是目前太难了。降低活化能也可以，μ子催化就是一种方法，用质量巨大的μ子代替电子，可以形成半径极小的μ原子，很容易聚变，就是μ子寿命太短太容易衰变了。目前全是暴力加温加压，但是加压太难了，主要是加温，但是聚变率始终提不上来。这很大程度上和等离子体物理有关，等离子体属于流体，流体的复杂与混沌是极难解决的，而等离子体还受电磁场影响，太复杂了，压力一高、约束磁场一小就转捩了，很难解决。而惯性约束要制造靶丸的缺陷难以解决，Z箍缩有是死路，太难了。我认为这极有可能是我们的宇宙最大的恶意——大过滤器，毁灭了无数文明。文明一旦耗尽资源而没有走向星空，世界末日就来了，文明哪怕看上去还在也只是死了没埋而已。可控核聚变刻不容缓啊。